1 other optimization that i'm adding, is approximating the face normal better. It is possible that polygon is not entirely flat. (See attached image) I will be using the method on right. These indices can be count like:
I figured that 5 vertex polygon is smallest one to benefit from this change. It is possible that 3 periodic vertices are in line formation too, and in that case, the left side method (0, 1, 2) would make a really bad normal approximation.Code:p0 = 0 p1 = 1+Count div 5 p2 = Count-1-Count div 5



 Reply With Quote
Reply With Quote
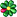
 It wasn't straightforward to come up with pattern that cover all polygon sizes, including triangles.
It wasn't straightforward to come up with pattern that cover all polygon sizes, including triangles.
Bookmarks